DAX et le contexte de filtre
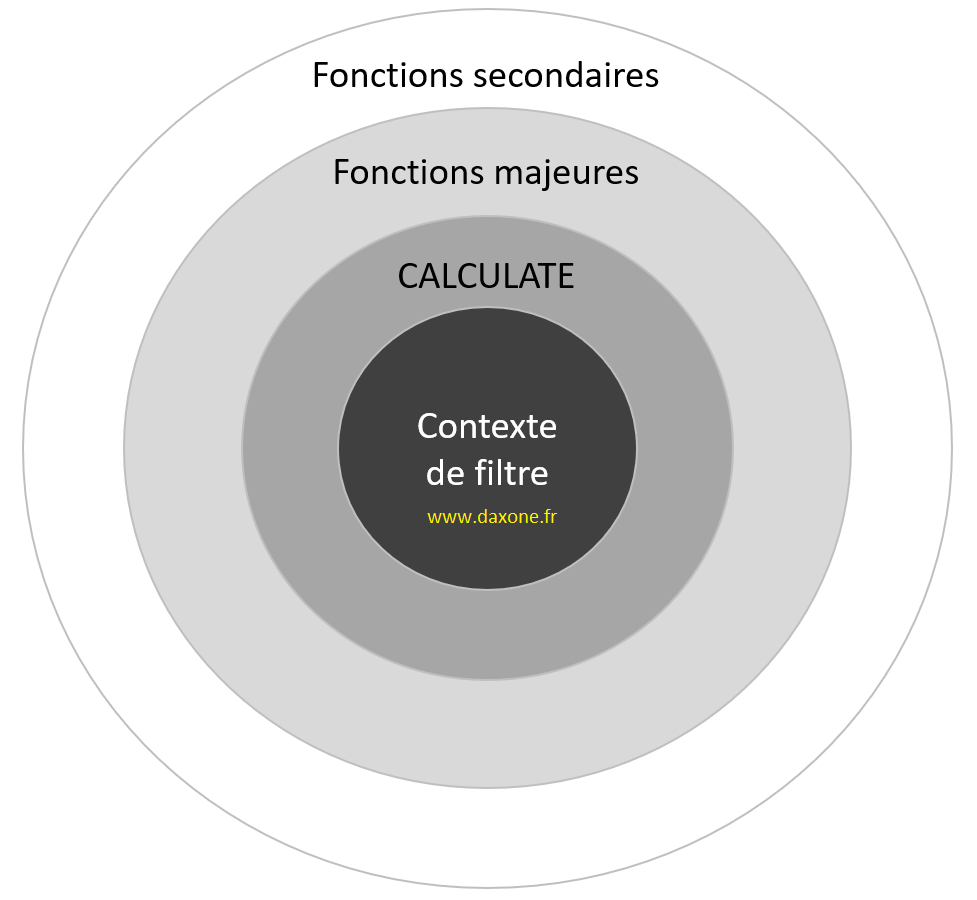
Pour moi, les choses sont claires : au cœur du DAX, il y a le contexte de filtre ; autour de ce cœur, il y a la fonction Calculate – la fonction la plus importante du DAX, la seule capable de modifier le contexte de filtre. Et autour, il y a le reste des fonctions DAX
La formule que je vous propose de commenter ici ne contient pas de Calculate, mais vous allez voir que le contexte de filtre intervient quasiment à chaque ligne, et qu’une bonne compréhension de son état est nécessaire pour composer la formule d’ensemble
Le modèle et le tableau
Je me sers d’un modèle très simple, puisqu’il s’agit d’une seule grande table :
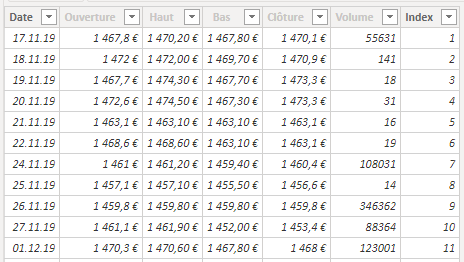
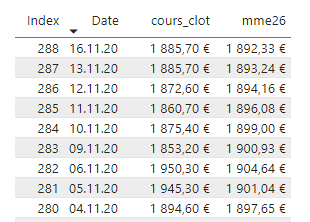
Et le visuel dans lequel sera affichée la mesure est lui aussi simple : un tableau avec l’index, la date et le cours de clôture. La mesure a pour but de calculer la moyenne mobile exponentielle (ou pondérée) – voir mon article du 17 novembre Construire et lire une moyenne mobile pour plus de détails :
La formule commentée
Voici d’abord la formule dans son ensemble :

Et maintenant pour un commentaire ligne à ligne :
mme26 =
La mesure est utilisée dans un tableau construit à partir de l’index et de la date. Sur la première ligne du tableau, le contexte de filtre contient donc 288 et 16-11-20
VAR longueur = 26
Cette première variable est une constante, le contexte de filtre n’entre donc pas en ligne de compte
VAR ref = max(prix_or_1an[Index])
Une variable est toujours évaluée au moment où elle est déclarée (donc pas au moment où elle est utilisée). max(prix_or_1an[Index]) est donc évaluée dans le contexte « 288 / 16-11-20 ». Dans ce contexte, il n’y a qu’une seule valeur de l’index, donc le MAX de cet index est « 288 ».
Notez que la raison pour laquelle on utilise la fonction MAX tient au fait que la mesure pourrait être affichée dans un tableau au niveau mois ou année : MAX récupère donc la valeur la plus récente, ce qui est cohérent avec le fonctionnement standard de Power BI.
VAR periode =
FILTER(
ALL(prix_or_1an)
, prix_or_1an[Index] > ref – longueur
&& prix_or_1an[Index] <= ref
)
Ici, les choses se corsent. Notez d’abord que la variable periode est une table. Je vous rappelle qu’à ce stade le contexte de filtre contient toujours « 288 / 16-11-20 ». FILTER est une fonction itérative, elle parcourt donc ligne à ligne la table qui lui est fournie en premier argument – dit autrement, elle introduit un contexte de ligne.
Dans l’argument de FILTER, ALL(prix_or_1an), ALL a pour effet de supprimer le contexte de filtre : donc exit « 288 / 16-11-20 », le contexte de filtre est vide. FILTER va donc parcourir toute la table prix_or_1an, et pour chaque ligne de cette table, va examiner la condition qui lui est fournie en deuxième argument. Le résultat, c’est que seules 26 lignes de la table initiale répondent aux conditions.
Notez que quelque soit la ligne du tableau sur laquelle nous nous trouvons, la variable periode aura toujours la même valeur (les mêmes 26 lignes). C’est le but, évidemment.
A la fin du calcul de periode, nous retrouvons le contexte initial : « 288 / 16-11-20 ». Je vais commenter ligne à ligne la variable suivante, où il se passe beaucoup de choses :
VAR resultat =
IF(
IF est une fonction itérative, elle introduit donc un contexte de ligne
COUNTROWS(periode) = longueur
COUNTROWS est une fonction agrégative, elle ignore par conséquent le contexte de ligne introduit par IF, et elle compte donc le nombre de ligne de la table periode
, SUMX(
Periode
SUMX est une fonction itérative. Elle va donc parcourir chaque ligne de periode complète (calculée une fois pour toute au-dessus, donc pas soumise au contexte de filtre « 288 / 16-11-20 ») pour calculer le cours pondéré, et introduit un contexte de ligne. A cet endroit de la formule, le contexte de filtre a changé : c’est maintenant celui qui est défini par la première ligne de la table periode – dans notre exemple, la ligne où l’index est égal à 259 (288 – 30, où 288 fait partie du résultat)
, VAR ponderation = longueur - (ref - prix_or_1an[Index]) RETURN
Là, nous avons un évènement moins courant : une variable est définie à l’intérieur d’un calcul. La variable étant évaluée dans le contexte où elle est définie, la pondération est calculée par rapport à l’index 259
prix_or_1an[cours_clot] * ponderation
Pour chaque ligne de la table periode, le cours est multiplié par la pondération – différente à chaque fois, puisque SUMX parcourt chaque ligne de periode
)
Ici, SUMX fait la somme des cours pondérés
/
SUMX(
periode
, longueur - (ref - prix_or_1an[Index])
)
)
Et là encore, SUMX fait la somme des cours pondérés sur la table periode complète, non soumise au contexte de filtre « 288 / 16-11-20 »
RETURN resultat
Le résultat, la moyenne mobile exponentielle (pondérée) est retournée, puis DAX passe à la ligne suivante du tableau, où le contexte de filtre devient « 287 / 13-11-20 »
Conclusion
Au terme de cet article, je tiens à souligner l’importance d’une bonne lecture du contexte de filtre : toute la réussite de votre formule repose sur votre perception de ses évolutions